While I can't say why I'm on his bent of posting about thermally related posts something that has bounced around in my brain for a while, is how can the death star manage to not liquefy itself when it fires its super laser.
For background, according to some calculations done by individuals far more skilled than I have calculated that it takes roughly 10^32 Joules of energy to destroy an Earth sized planet, it is also estimated that all of this energy is expended in roughly one second, meaning the Death Star expends 10^32 watts. According to Wookiepedia it takes roughly 24 hours to recharge this supremely powerful weapon. The underlying question I have as an engineering geek is this, how efficient is the Death Star's heat management system to allow for it to operate while allowing for a living and breathing crew of over one million Storm Troopers, fighter pilots, bar tenders, bureaucrats, etc...
While I unfortunately don't have a data base of materials that are available to engineers in the Star Wars universe we can provide ourselves with some critical data necessary for calculations.
First we have a minimum power output of the Death Star's primary reactor system(s) I say minimum power output as it is not unreasonable to assume that the Death Star's other systems could be powered by these primary generator array (hard core Star Wars fanboys, please tell me about any incorrect assumptions that I might have made, long ago I erred from the true path and some details are still a bit too hazy)
This can be relatively simply calculated from the known recharge time, 24 hours, and the energy output calculated by Michael Wong of Stardestroyer.net, For personal ease I am only making the calculations necessary for the Death Star seen in Star Wars a New Hope, that being said the only a few variables would require changing to accommodate the second Death Star, the original prototype or any other number of super-laser based weapons of the Star Wars universe.
Minimum Power Output of Generator = (Energy output of Super Laser Array)(unit of Joules)/(Total Recharge time)(Seconds)
(10^32)Joules/(24(Hour)*(3600 (Seconds/Hour)= (10^32 Joules ) / (8.64*10^4 Seconds)=Min Pout
1.15741*10^27 Watts=Minimum Power Output of Generator
Right now I will do a really quick and dirty calculation and estimate the minimum temperature of tpoint and just go off the trench run briefing scene, where they explain that all of the Death Star's waste heat is dumped through a thermal exhaust port 2 meters wide and circular in shape. Using the equations for black body radiation we can calculate the theoretical temperature at said exhaust port.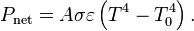
, Pnet=1.15741*10^27 watts : A= π*(Diameter/2)^2=π*(2m/2)^2=3.141592653 m^2 : σ=Boltzmann Constant=1.3806503 × 10-23 w/[(m^2)*(K^4)]: ε= is the emissivity of a given material, for ease of calculation we will assume that the value is 1: To is the temperature of space and we will assume that it is 10 degrees Kelvin
substituting the variables with the above numbers
1.15741*10^27 watts=3.141592653 (m^2)*1.3806503 × 10-23 w/[(m^2)*(K^4)]*1*[(Tport)^4-(10K)^4]
this reduces to
(1.15741*10^27 watts)/{3.141592653 (m^2)*1.3806503 × 10-23 w/[(m^2)*(K^4)]}=[(Tport)^4-(10K)^4]
becomes
[2.668410821*(10^49)*(K^4)]-[10*(10^3)*(K^4)]=(Tport)^4
Taking the fourth root of both sides of the equation
we are left with the Temperature of the Death Star's Exhaust Port
T port = 2.273*(10^12)K or two trillion two hundred seventy three billion degrees Kelvin. For comparison most Earthly materials break down well before 6*(10^3)K or 6000 degrees for those who dislike using scientific notation. At temperatures like those, the photon torpedoes launched by Luke Skywalker are unlikely to have even gotten within several hundred meters of the exhaust port, let alone close enough to explode within the structure of the Death Star.
What follows below will evolve into some follow up calculations as how the Death Star might work if it didn't rely on that one exhaust port to maintain system stability.
Follow Up Math (Nov 17, 2012)
After posting this article on Reddit one reader pointed out that I was treating the entire generator as a straight heat source, which is bad modelling on my part. As I said on Reddit I was tired the day I made this post originally that being said I should attach a range of corrections and modeling options..
The first is simply considering the system efficiency in making calculations.
To make the math easier, and because I have no way of even remotely accurately modeling the Death Star Super Laser System's (this includes the net efficiency of the firing mechanism, the generators, and the energy storage facilities within the Death Star) we are treating system efficiency as a single variable.
The general Form
System Efficiency=X
System Power Production Requirements= (Theoretical Minimum Power Output of Generator)/(System Efficiency)
Waste Heat Produced =(System Power Production Requirements)-(Theoretical Minimum Power Output of Generator)
Waste Heat Produced is now fed back into the black body radiation calculations
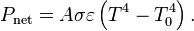
For Different Efficiencies and Radiator Surface Areas
X=50% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 2.27*10^12 degrees Kelvin
X=90% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 1.31*10^12 degrees Kelvin
X=99.999 999 999% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 4.04*10^9 degrees Kelvin
X=99.999 999 999 999% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 7.18*10^8 degrees Kelvin (Still really damn hot)
X=99.999 999 999 999 999% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 3.99*10^8 degrees Kelvin (Still really damn hot and Microsoft Excel won't let me look at anything more efficient)
Ok, so what would it look like if we said that the Death Star had the the entirety of its surface area (as a smooth sphere) turned into a black-body radiator
The Death Star is 160 km in diameter, so its surface area is roughly
(80,000m)^2*3.14159265= 80,424,771,917 m^2 : so pretty darn big
X=50% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be as originally calculated 5.68*10^9 degrees Kelvin
X=90% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 3.28*10^9degrees Kelvin
X=99.999 999 999% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 1.01*10^7 degrees Kelvin
X=99.999 999 999 999% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 1.8*10^6 degrees Kelvin (Still really damn hot and microsoft Excel won't let me look at anything more efficient)
And now for the final random calculations. A friend of mine put forth the question
Lets assume Vader has some super material for his exhaust, that can take temps of 20k° K.
How big would the exhaust have to be in order to not melt, and how does that size relate to the Death Stars size?
Now we are approaching the calculations from a different perspective, where the surface area of the object is unbound, but the temperature of the system is now restricted
in the rough form we see
Qwaste heat=Aradiator system*Boltzman Constant*(Tradiator^4-Tvacuum^4)
Ok I'm going to take a breather for a bit updates later
For background, according to some calculations done by individuals far more skilled than I have calculated that it takes roughly 10^32 Joules of energy to destroy an Earth sized planet, it is also estimated that all of this energy is expended in roughly one second, meaning the Death Star expends 10^32 watts. According to Wookiepedia it takes roughly 24 hours to recharge this supremely powerful weapon. The underlying question I have as an engineering geek is this, how efficient is the Death Star's heat management system to allow for it to operate while allowing for a living and breathing crew of over one million Storm Troopers, fighter pilots, bar tenders, bureaucrats, etc...
While I unfortunately don't have a data base of materials that are available to engineers in the Star Wars universe we can provide ourselves with some critical data necessary for calculations.
First we have a minimum power output of the Death Star's primary reactor system(s) I say minimum power output as it is not unreasonable to assume that the Death Star's other systems could be powered by these primary generator array (hard core Star Wars fanboys, please tell me about any incorrect assumptions that I might have made, long ago I erred from the true path and some details are still a bit too hazy)
This can be relatively simply calculated from the known recharge time, 24 hours, and the energy output calculated by Michael Wong of Stardestroyer.net, For personal ease I am only making the calculations necessary for the Death Star seen in Star Wars a New Hope, that being said the only a few variables would require changing to accommodate the second Death Star, the original prototype or any other number of super-laser based weapons of the Star Wars universe.
Minimum Power Output of Generator = (Energy output of Super Laser Array)(unit of Joules)/(Total Recharge time)(Seconds)
(10^32)Joules/(24(Hour)*(3600 (Seconds/Hour)= (10^32 Joules ) / (8.64*10^4 Seconds)=Min Pout
1.15741*10^27 Watts=Minimum Power Output of Generator
Right now I will do a really quick and dirty calculation and estimate the minimum temperature of tpoint and just go off the trench run briefing scene, where they explain that all of the Death Star's waste heat is dumped through a thermal exhaust port 2 meters wide and circular in shape. Using the equations for black body radiation we can calculate the theoretical temperature at said exhaust port.
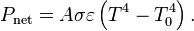, Pnet=1.15741*10^27 watts : A= π*(Diameter/2)^2=π*(2m/2)^2=3.141592653 m^2 : σ=Boltzmann Constant=1.3806503 × 10-23 w/[(m^2)*(K^4)]: ε= is the emissivity of a given material, for ease of calculation we will assume that the value is 1: To is the temperature of space and we will assume that it is 10 degrees Kelvinsubstituting the variables with the above numbers
1.15741*10^27 watts=3.141592653 (m^2)*1.3806503 × 10-23 w/[(m^2)*(K^4)]*1*[(Tport)^4-(10K)^4]
this reduces to
(1.15741*10^27 watts)/{3.141592653 (m^2)*1.3806503 × 10-23 w/[(m^2)*(K^4)]}=[(Tport)^4-(10K)^4]
becomes
[2.668410821*(10^49)*(K^4)]-[10*(10^3)*(K^4)]=(Tport)^4
Taking the fourth root of both sides of the equation
we are left with the Temperature of the Death Star's Exhaust Port
T port = 2.273*(10^12)K or two trillion two hundred seventy three billion degrees Kelvin. For comparison most Earthly materials break down well before 6*(10^3)K or 6000 degrees for those who dislike using scientific notation. At temperatures like those, the photon torpedoes launched by Luke Skywalker are unlikely to have even gotten within several hundred meters of the exhaust port, let alone close enough to explode within the structure of the Death Star.
What follows below will evolve into some follow up calculations as how the Death Star might work if it didn't rely on that one exhaust port to maintain system stability.
Follow Up Math (Nov 17, 2012)
After posting this article on Reddit one reader pointed out that I was treating the entire generator as a straight heat source, which is bad modelling on my part. As I said on Reddit I was tired the day I made this post originally that being said I should attach a range of corrections and modeling options..
The first is simply considering the system efficiency in making calculations.
To make the math easier, and because I have no way of even remotely accurately modeling the Death Star Super Laser System's (this includes the net efficiency of the firing mechanism, the generators, and the energy storage facilities within the Death Star) we are treating system efficiency as a single variable.
The general Form
System Efficiency=X
System Power Production Requirements= (Theoretical Minimum Power Output of Generator)/(System Efficiency)
Waste Heat Produced =(System Power Production Requirements)-(Theoretical Minimum Power Output of Generator)
Waste Heat Produced is now fed back into the black body radiation calculations
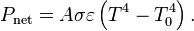
For Different Efficiencies and Radiator Surface Areas
X=50% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 2.27*10^12 degrees Kelvin
X=90% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 1.31*10^12 degrees Kelvin
X=99% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 7.21*10^11 degrees Kelvin
The radiator temperature will be as originally calculated 7.21*10^11 degrees Kelvin
X=99.9% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 4.04*10^11 degrees Kelvin
The radiator temperature will be as originally calculated 4.04*10^11 degrees Kelvin
X=99.999 999 999% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 4.04*10^9 degrees Kelvin
X=99.999 999 999 999% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 7.18*10^8 degrees Kelvin (Still really damn hot)
X=99.999 999 999 999 999% Area of the Radiator=3.14 square meters
The radiator temperature will be as originally calculated 3.99*10^8 degrees Kelvin (Still really damn hot and Microsoft Excel won't let me look at anything more efficient)
Ok, so what would it look like if we said that the Death Star had the the entirety of its surface area (as a smooth sphere) turned into a black-body radiator
The Death Star is 160 km in diameter, so its surface area is roughly
(80,000m)^2*3.14159265= 80,424,771,917 m^2 : so pretty darn big
X=50% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be as originally calculated 5.68*10^9 degrees Kelvin
X=90% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 3.28*10^9degrees Kelvin
X=99.9% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 1.01*10^9 degrees Kelvin
The radiator temperature will be 1.01*10^9 degrees Kelvin
X=99.999 999 999% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 1.01*10^7 degrees Kelvin
X=99.999 999 999 999% Area of the Radiator=80.4*10^9 square meters
The radiator temperature will be 1.8*10^6 degrees Kelvin (Still really damn hot and microsoft Excel won't let me look at anything more efficient)
And now for the final random calculations. A friend of mine put forth the question
Lets assume Vader has some super material for his exhaust, that can take temps of 20k° K.
How big would the exhaust have to be in order to not melt, and how does that size relate to the Death Stars size?
Now we are approaching the calculations from a different perspective, where the surface area of the object is unbound, but the temperature of the system is now restricted
in the rough form we see
Qwaste heat=Aradiator system*Boltzman Constant*(Tradiator^4-Tvacuum^4)
Ok I'm going to take a breather for a bit updates later
No comments:
Post a Comment